Estimation of the Deformation Gradient Tensor by Particle Tracking Near a Free Boundary with Quantified Error

Abstract

Background

Obtaining accurate displacement measurements for large material deformation and/or rotation presents a distinct challenge to digital image correlation (DIC) due to cumulative and decorrelation errors, particularly near material boundaries.

Objective

We aim to accurately measure the deformation gradient tensor near boundary discontinuities in situations of large deformation and large deformation gradients.

Methods

To achieve this goal, the locations of randomly distributed particles are tracked using an open-source particle-tracking software, Trackpy. A least-squares estimate of the deformation gradient tensor field uses nearest-neighbor material vectors and a first-order Finite Difference (FD) approximation, circumventing common errors in other methods. The error caused by FD approximation and that incurred by measurement are derived and tested with exhaustive numerical simulations. Furthermore, a uniaxial tensile test and mode-I fracture experiment are conducted with particle-embedded hydrogels to validate the method.

Results

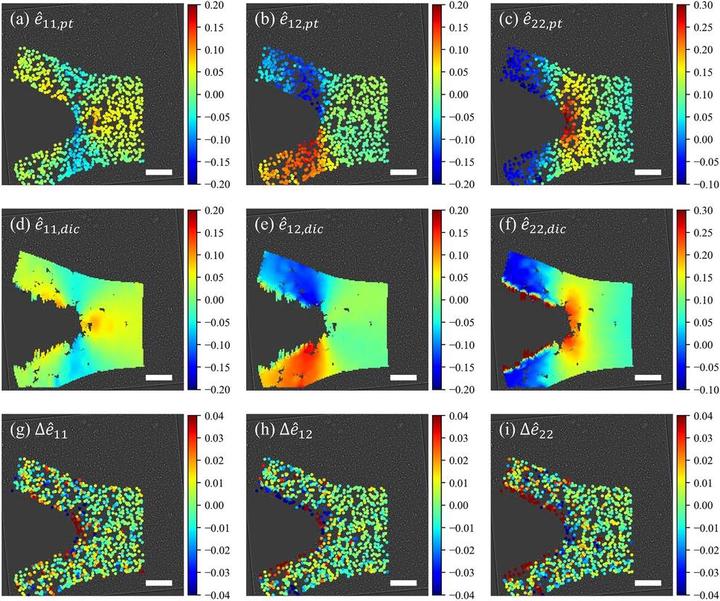
Numerical results corroborate a theoretical expression of measurement error. They show that the FD error increases while the measurement error decreases for a growing estimating radius. Moreover, measurement error is linearly correlated to displacement noise. A benchmark uniaxial tensile test validates the accuracy of the proposed estimator, and the near-crack-tip measurements in a tensile fracture experiment demonstrate the estimator’s capabilities near a free surface, when a material undergoes large deformation and rotation. The results of the displacement and strain data are benchmarked against kinematic data obtained using an open-source DIC software, Ncorr. Computation time for both methods is compared.

Conclusions

A deformation gradient tensor estimator is developed based on a particle tracking technique and a least squares routine. Theoretical error bounds on the estimator are verified by numerical simulations, and the method’s capability is confirmed by physical experiments in evaluating large deformation and rotation near a free boundary. The proposed estimator is expected to open a door towards future material tests and experimental mechanics studies, especially in large deformation and large rotation scenarios.